电脑有什么用(1_数值计算软件Octave在分期问题中的应用举例)

隐私提示:本站使用Microsoft Clarity统计访客信息,关于我将收集你的具体何种信息及如何禁止我收集你的信息请点击这里.

  “电脑有什么用？”，为了回答这个问题笔者计划先举一个电脑的用途实例。读者需要注意本例为完全虚构的场景。读者可以从这个链接获得本文中提到的软件安装程序，还没有电脑或电脑还不能正常使用的读者也请不要担心，这只是一个快速入门的应用举例，之后的文章中笔者可能与读者一起讨论如何选择并配置好自己的第一台笔记本计算机。
  这里假设读者非常心水IBM公司最新推出的5100型号笔记本计算机(注解：世界上第一款商用笔记本计算机，见下图)，IBM公司在其网上商城推出了分期购物免息活动。读者经过研究发现，该公司售卖的5100笔记本计算机可以在其商城中选择多种不同的搭配选项，但不同搭配间差价很大。同时，读者也注意到A网上购物平台现在也在进行立减100元促销活动。最终读者期待了解到以下两种购买方式对于还未选定的电脑，何种能够使读者节省更多的货币。

    1.使用IBM公司网上商城提供的24期免息分期服务。将还没有还款的货币存入B金融公司的基金账户，每月可得到年化收益率为2.7%的利息;
    2.使用A网购平台的立减100元服务，货款一次性付清。
    这里假设两种方式均由卖家承担邮费，且可以选择同种搭配选项的电脑，商品定价也完全相同。
  由于采用分期方式时，读者每月基金账户的资本都将减少，因此每月利息收益将发生变化。读者经过分析，在草稿纸上通过下面的累加计算快速得到了第一种方式的预期利息收益，并很快与第二种方式进行了损益对比，获得了一个价格阈值。读者自豪地宣称：当选购大于该价格的机器时，采用免息分期付款更合适，反之选择立减服务。

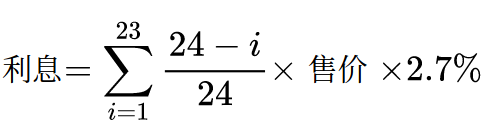
  这对于笔者而言实在有些难度，于是笔者计划使用GNU Octave程序(一款数值计算程序)编程解决这个问题。需要注意的是，这个举例并不那么好，对于数学基础扎实的读者将立马看出这是一个算术级数。但这并不妨碍本例成为”电脑有什么用”这个问题的解答举例。
  需要提醒读者，GNU Octave是一款数值计算程序，被设计用于工程学用途，大部分情况下无法求出问题的精确解。对于向往精确解计算的读者，请参考符号计算程序Maxima项目的主页，这不是本次讨论的内容。
  笔者经历了一番较长时间的研究，终于编写了下面的小程序。需要提醒的是，读者不必了解Octave程序的语法，只需要根据笔者注释的内容(百分号后的内容)感受计算过程即能满足本文编写的初衷。该程序能够很快给出不同利率、立减、分期时间等情况下的价格阈值。这相对于刚才那个聪明的读者而言具有一个很明显的优势，即在不同参数情况时只需要修改程序中的数据就能很快获得结果，这是笔算无法比拟的。

    clc,clear;          %如果事先运行过其他Octave程序，应该先使用这句话清楚之前的计算结果;  
                        %换行在计算机程序编写过程中是非常有用的分隔符，可以帮助编码者快速理清程序结构;  
    profit_rate=2.7;    %这是一个等式，本质上是让"profit_rate"这个表示利率的变量等于2.7;  
    cut_down=100;       %立减金额。大部分程序编码时的变量名可以根据编码者喜好决定;  
    price_start=0;      %求解价格的最小值。也就是程序尝试比价的开始价格，这样的边界数据对于数值计算软件是必要的;  
    price_end=10000;    %求解价格的最大值。数值计算软件并不能真的求解表达式，这里它将一个价格一个价格进行计算和比较;  
    price_step=1;       %求解价格的分度值。程序将在价格最小值到最大值范围内，每隔这个数求解一次;  
    total_month=24;     %分期的月数;  
        %可以不用拉丁字母给变量其名吗？这个问题是否定的。但其原因不在今天的讨论范围中;  
    for price=price_start:price_step:price_end      %这是一个控制语句，表示在价格最小值到最大值中，每隔一个分度值给价格换一个值重新求解;  
        profit=0;                                   %因为利息是累加的，因此每次更改价格都将从0开始累加;  
        for month=1:total_month-1                   %按月累加利息，这里省略了一个冒号。事实上不指定分度值的情况下，Octave程序将自动以1作为分度值;  
            profit=profit+(total_month-month)/total_month*price*(profit_rate/100/12);  
                                                    %这里笔者直接借鉴了之前那位读者的表达式;  
        end                                         %对于需要一遍又一遍进行的计算过程，Octave需要知道它要循环计算的部分在哪里结束，这个end就写的很清楚;  
        sel1=price-profit;                          %计算第一种方案的实际付出;  
        sel2=price-cut_down;                        %第二种方案;  
        if(sel1<sel2)               %比较分期付款是否划算;  
            break;                  %如果分期付款开始变得划算了，那就表示已经达到阈值，此时结束循环，价格数据将保持不变，我们只需要将它输出到显示器上就好了;  
        end                         %对于这种有条件进行的计算，Octave也需要知道符合条件时它需要在哪里结束计算;  
    end     %每一个end都对应于它所负责的区域，这个区域总是在它和最近的一个没有配对的需要end的语句中间;  

    fprintf(["Price Threshold: ", num2str(price),"\n"]);    %将这个阈值价格显示出来;  

  在将程序输入GNU Octave程序后，笔者在”Octave:8>”之后的得到了阈值数据价格为3865。细心的读者可能会注意到笔者在第一行代码前添加了百分号，这是为了截取到完整的运行实例而加入的，读者并不需要这么做。

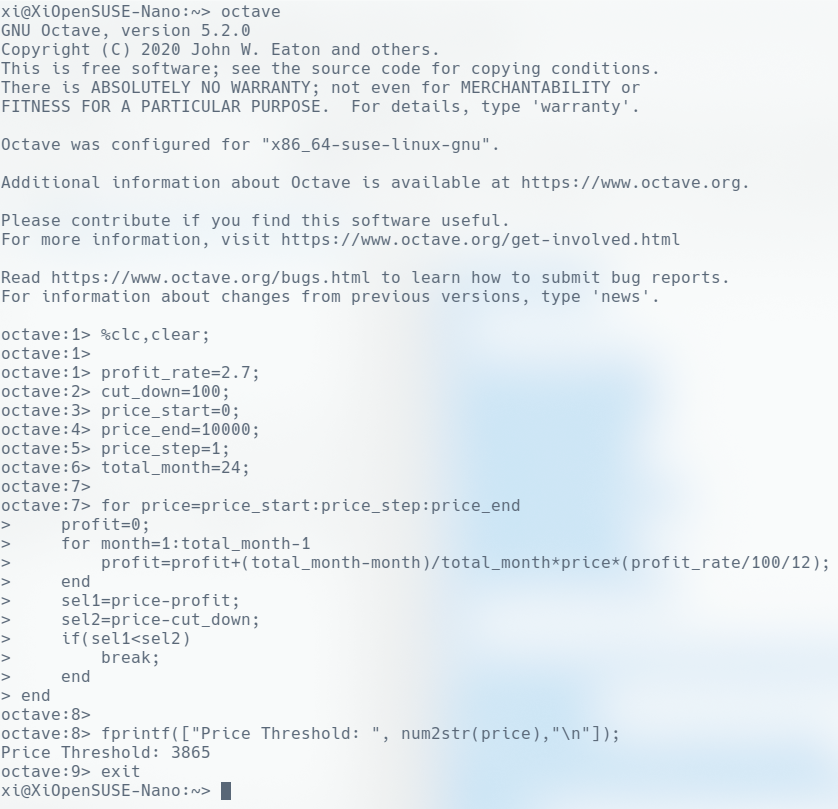
  随后笔者对这个计算程序进行了计时运行，它仅使用0.65447秒就求解了3865组不同的价格，并将作为分界线的那个价格现实到显示器上。随后笔者尝试计时笔算求解这个结果(不同于这个程序，笔者是笔算算术级数并求解不等式)，最终用时为260.81秒(笔者计算水平不高)。笔者编写这个程序花费了79.57秒，这么看来编码所耗费的时间都不值一提。
  如果修改求解分度值到0.01,将得到更加精确的3864.74。程序计算所消耗的时间将被大幅提升到64.821秒，当然这依然较笔算用时更短。考虑到参数可以修改，程序可以重复利用，真的非常令人激动。
  读者可以尝试修改不同的参数自行运行程序观察效果，考虑到0.655秒笔者的老款笔记本电脑就能求解3865组不同价格，稍微更接近本质的说法是104361次计算，相当于每秒能计算16万次。这是非常令人感到激动的。
  本文到这里就告一段落了，耐心的读者请期待笔者下一次更新吧。

  

UMRAY

2021.08.23